សេចក្តីផ្តើមនៃ Multi-Armed Bandit

ក្នុងអត្ថបទនេះ ខ្ញុំនិងបរិយាយព័ត៌មានទាក់ទងនឹង MAB ដោយចាប់ផ្តើមពីការពន្យល់ពីនិយមន័យ និងប្រវត្តិសង្ខេបនៃ MAB ក្នុងផ្នែកទី១។ ផ្នែកទី២បកស្រាយអំពីទ្វេគ្រោះនៃការរុករកនិងការចំរាញ់ (Exploration-Exploitation Dilemma)។ ផ្នែកទី៣នឹងក្តោបលើរង្វាស់រង្វាល់គុណភាពនៃប្រមាណវិធី (Algorithm) ដែលដោះស្រាយបញ្ហា MAB ។ ខ្ញុំនឹងសង្ខេបអត្ថបទឡើងវិញក្នុងផ្នែកទី៤

Multi-armed bandit (MAB) គឺជាបញ្ហាគណិតវិទ្យាមួយដែលត្រូវបានសិក្សាយ៉ាងស៊ីជម្រៅ និងប្រើប្រាស់យ៉ាងទូលំទូលាយ។ MAB ត្រូវបានផ្តួចផ្តើមដំបូងក្នុងសហគមន៍អ្នកស្រាវជ្រាវតាំងពីឆ្នាំ១៩៣៣មកម៉្លេះ (Thompson 1933) ហើយនៅតែបន្តត្រូវបានគេសិក្សារហូតមកដល់សព្វថ្ងៃ (Simchi-Levi and Wang 2023)។ MAB គឺជាគម្រូលេខនៃបញ្ហារស់នៅក្នុងជីវិតយ៉ាងច្រើនដូចជា ការសាកឃ្លីនិក (Clinical Trial (Thompson 1933)) ប្រព័ន្ធផ្តល់យោបល់ (Recommendation system (Lattimore and Szepesvári 2020)) និងការដាក់ផ្សព្វផ្សាយពាណិជ្ជកម្ម (Advert Placement (Lattimore and Szepesvári 2020)) ជាដើម។ នេះបញ្ជាក់ថា MAB គឺជាបញ្ហាមួយដ៏សំខាន់ដែលយើងទាំងអស់គ្នាគួរតែយកចិត្តទុកដាក់ស្វែងយល់។

ក្នុងអត្ថបទនេះ ខ្ញុំនិងបរិយាយព័ត៌មានទាក់ទងនឹង MAB ដោយចាប់ផ្តើមពីការពន្យល់ពីនិយមន័យ និងប្រវត្តិសង្ខេបនៃ MAB ក្នុងផ្នែកទី១។ ផ្នែកទី២បកស្រាយអំពីទ្វេគ្រោះនៃការរុករកនិងការចំរាញ់ (Exploration-Exploitation Dilemma)។ ផ្នែកទី៣នឹងក្តោបលើរង្វាស់រង្វាល់គុណភាពនៃប្រមាណវិធី (Algorithm) ដែលដោះស្រាយបញ្ហា MAB ។ ខ្ញុំនឹងសង្ខេបអត្ថបទឡើងវិញក្នុងផ្នែកទី៤។

Multi-armed bandit ជាអ្វី?

សូមពិចារណាបញ្ហាដូចតទៅនេះ។ ស្រមៃថាអ្នកត្រូវការសម្រេចចិត្តម្តងហើយម្តងទៀត ដោយជ្រើសរើស \(1\) ក្នុងជម្រើស \(k\)។ ក្រោយការសម្រេចចិត្តម្តងៗ អ្នកអាចទទួលបានរង្វាន់ដែលមានលក្ខណៈចៃដន្យ ហើយភាពចៃដន្យនេះអាស្រ័យលើជម្រើសរបស់អ្នក។ អ្នកមានគោលបំណងបង្កើនមធ្យមនៃរង្វាន់សរុបទទួលបានអោយដល់អតិបរមា ដោយកំហិតថាចំនួនសម្រេចចិត្តមានកំណត់ ឧទាហរណ៍អ្នកអាចសម្រេចចិត្តបានតែមួយពាន់ដង ឬមួយពាន់ជំហានជាដើម។

នេះជាទម្រង់ដើមនៃបញ្ហា \(k\)-armed bandit ដែលឈ្មោះនេះយកតាមម៉ាស៊ីនល្បែងក្នុងកាស៊ីណូដូចក្នុងរូបទី១ (Figure 1) ប៉ុន្តែប្តូរពីជួរមាន \(k\) ម៉ាស៊ីនដៃ \(1\) មកជាម៉ាស៊ីនមួយមានដៃ \(k\) វិញ។ ការសម្រេចចិត្តម្តងៗគឺដូចជាការដាក់កាក់ទាញដៃណាមួយនៃម៉ាស៊ីននេះ ហើយការផ្តល់រង្វាន់ប្រៀបដូចជាម៉ាស៊ីននេះទម្លាក់លុយ (hit the jackpot) អុីចឹង។ តាមរយៈការលេងម្តងហើយម្តងទៀត អ្នកនឹងចំណាយកាក់ទាញតែដៃណាមួយគត់ដែលតែងតែទម្លាក់លុយច្រើននិងញឹកញាប់ជាងគេ។

Figure 1: រូបទី១៖ ជួរម៉ាស៊ីនដាក់កាក់ទម្លាក់លុយនៅរដ្ឋឡាសវេហ្គាស សហរដ្ឋអាមេរិច (តំណ)

ដើម្បីសម្រួលដល់ការស្វែងយល់ ខ្ញុំនឹងប្រើប្រាស់ម៉ូដែលគណិតវិទ្យាសម្រាប់ \(k\)-armed bandit ដូចតទៅ។ សន្មត់ថាម៉ាស៊ីនអាចទម្លាក់រង្វាន់ \(1\) ឯកតា ឬ \(0\) ឯកតា ដែលឱកាសទម្លាក់រង្វាន់ \(1\) ប្រែប្រួលតាមដៃនិមួយៗ និងសន្មត់ថាយើងអាចលេងបានតែ \(T\in\mathbb{N}\setminus\\{0\\}\) ជំហានប៉ុណ្ណោះ ។ យើងតាង \(\mu_i\) ជាឱកាស ឬតម្លៃសង្ឃឹម (ត្រង់នេះ ឱកាស និងតម្លៃសង្ឃឹមស្មើគ្នាក៏ព្រោះតែអថេរចៃដន្យមានរបាយ Bernoulli ហើយគេប្រើប្រាស់ តម្លៃសង្ឃឹម ក្នុងការអនុវត្តផ្លូវការ ប៉ុន្តែខ្ញុំប្រើប្រាស់ ឱកាស ដើម្បីជួយសម្រួលដល់ការពន្យល់របស់ខ្ញុំប៉ុណ្ណោះ) ដែលដៃ \(i\) ធ្វើអោយម៉ាស៊ីនទម្លាក់រង្វាន់ \(1\) ហើយតាង \(r_t\in\\{0,1\\}\) ជារង្វាន់ដែលទទួលបាននៅជំហាន \(t\) ដែល \(1\le t\le T\)។ រង្វាន់សរុបបន្ទាប់ពីលេងបាន \(T\) ជំហានគឺ \(\sum_{t=1}^T r_t\)។ ដោយសន្មត់ថាពេលចាប់ផ្តើមលេង យើងមិនស្គាល់អំពីតម្លៃ \(\\{\mu_i\\}_{1\le i\le k}\)ឡើយ យើងមានគោលបំណងប្រមូលជាអតិបរមា មធ្យមនៃរង្វាន់សរុបទទួលបានបន្ទាប់ពីលេងបាន \(T\) ជំហាន

\[\begin{equation} \mathbb{E}\left[ \sum_{t=1}^T r_t\right] \end{equation}\]

។ នេះជាម៉ូដែលគណិតវិទ្យាងាយមួយសម្រាប់បញ្ហា \(k\)-armed bandit។

ដោយសារម៉ូដែលគណិតវិទ្យាសម្រាប់បញ្ហា \(k\)-armed bandit មានលក្ខណៈសាមញ្ញ បញ្ហានេះត្រូវបានគេសិក្សា និងអនុវត្តយ៉ាងទូលំទូលាយ។ ការអនុវត្តក្លាសិកមួយគឺការសាកឃ្លីនិក (Clinical Trial (Thompson 1933)) ដែលគ្រូពេទ្យត្រូវសម្រេចចិត្តអោយថ្នាំ \(1\) ប្រភេទក្នុងចំណោមថ្នាំ \(k\) ប្រភេទទៅអ្នកជម្ងឺដើម្បីអោយគាត់បានជាសះស្បើយ។ ដោយប្រើថ្នាំប្រភេទ \(i\) អ្នកជម្ងឺមានឱកាសជាសះស្បើយ \(100\times\mu_i\) ភាគរយ។ គ្រូពេទ្យមានគោលបំណងអោយចំនួនអ្នកជម្ងឺជាសះស្បើយមានច្រើនអតិបរមា ប៉ុន្តែលោកចាប់ផ្តើមព្យាបាលដោយមិនស្គាល់តម្លៃឱកាស \(\mu_i\) ណាមួយឡើយ។ ការអនុវត្តមួយទៀតក្នុងសម័យឌីជីថល គឺការដាក់ផ្សព្វផ្សាយពាណិជ្ជកម្ម (Advert Placement (Lattimore and Szepesvári 2020)) ដែលម្ចាស់វេបសាយចង់លក់ផលិតផលមួយ ដោយដាក់វីដេអូ \(1\) ក្នុងចំណោមវីដេអូផ្សាយពាណិជ្ជកម្ម \(k\) អោយអ្នកប្រើប្រាស់ (User) មើល។ ក្រោយមើលវីដេអូ \(i\) អ្នកប្រើប្រាស់ចុចទិញដោយឱកាស \(100\times\mu_i\) ភាគរយ។ ចាប់ផ្តើមដោយមិនស្គាល់ពីតម្លៃនៃ \(\mu_i\) ណាមួយឡើយ ម្ចាស់វេបសាយមានគោលបំណងបង្កើនការលក់អោយបានអតិបរមា។ ទាំងនេះបញ្ជាក់ថា បញ្ហា \(k\)-armed bandit មានការអនុវត្តយ៉ាងច្រើន។

ប្រមាណវិធី (Algorithm)

ដោយមិនស្គាល់ពីតម្លៃសង្ឃឹម \(\\{\mu_i \\}_{1\le i\le k}\) យើងប្រឈមនឹងវិវាទការណ៍រវាងយុទ្ធសាស្រ្ត២គឺ ការរុករក (Exploration) និងការចំរាញ់ (Exploitation)។ ការរុករកអនុញ្ញាតអោយយើងប្រមូលព័ត៌មានដើម្បីប៉ាន់ប្រមាណតម្លៃសង្ឃឹមនៃដៃនិមួយៗអោយបានជាក់លាក់ ប៉ុន្តែបណ្តាលអោយយើងខាតជំហានព្រោះតែចំនួនជំហានសរុបមានកំណត់។ ចំណែកឯការចំរាញ់អនុញ្ញាតអោយយើងប្រើប្រាស់ព័ត៌មានប្រមូលបានដើម្បីប្រមាណថាដៃមួយណាមានតម្លៃសង្ឃឹមខ្ពស់ជាងគេ ប៉ុន្តែបណ្តាលអោយយើងសម្រេចចិត្តខុសនៅពេលដែលព័ត៌មានប្រមូលបានមិនទាន់គ្រប់គ្រាន់។ ជាឧទាហរណ៍ គ្រូពេទ្យអាចសាកថ្នាំនិមួយៗច្រើនដងដើម្បីដឹងពីប្រសិទ្ធភាពរបស់វា ប៉ុន្តែអាចបណ្តាលអោយមានចំនួនអ្នកជម្ងឺជាសះស្បើយតិច ដែលធ្វើអោយគ្រូពេទ្យនោះបាត់បង់កេរ្តិឈ្មោះ។ ម៉្យាងទៀត គ្រូពេទ្យអាចប្រើប្រាស់បទពិសោធន៍របស់គាត់ដើម្បីសម្រេចថាថ្នាំមួយប្រភេទណាមានប្រសិទ្ធភាពខ្ពស់ជាងគេ ប៉ុន្តែបើបទពិសោធន៍មិនគ្រប់គ្រាន់ នោះការសម្រេចចិត្តគាត់នឹងមិនត្រឹមត្រូវដែលបណ្តាលអោយមានចំនួនអ្នកជម្ងឺជាសះស្បើយតិចដូចគ្នា។ ជាទូទៅ វិវាទការណ៍នេះត្រូវបានគេអោយឈ្មោះថា ទ្វេគ្រោះនៃការរុករកនិងការចំរាញ់ (Exploration-Exploitation Dilemma)។

ជាធម្មតា ប្រមាណវិធីដែលយើងនឹកឃើញមុនគេសម្រាប់ដោះស្រាយបញ្ហា \(k\)-armed bandit គឺការសាកទាញដៃនិមួយៗដោយចំនួនថេរដងណាមួយ (រុករក) រួចគណនាតែម្តងគត់ថាដៃណាដែលមានមធ្យមសំណាក (sample average) ធំជាងគេ ហើយទាញតែដៃមួយនោះរហូតដោយមិនធ្វើការគណនាអ្វីទៀតឡើយ (ប្តូរផ្តាច់)។ គេអោយឈ្មោះប្រមាណវិធីនេះថា រុករករួចប្តូរផ្តាច់ (Explore-then-Commit, ETC)។ តែដោយទទួលដឹងអំពីទ្វេគ្រោះនៃការរុករកនិងការចំរាញ់ យើងអាចកែច្នៃប្រមាណវិធីខាងដើមដោយក្នុងប្រូបាប៊ីលីតេ \(\varepsilon\) ទាញដៃមួយដោយចៃដន្យដោយប្រូបាប៊ីលីតេឯកសណ្ឋាន និងក្នុងប្រូបាប៊ីលីតេ \(1-\varepsilon\) ទាញដៃដែលមានមធ្យមសំណាកធំជាងគេ។ ប្រមាណវិធីនេះមានឈ្មោះថា \(\varepsilon\)-Greedy ដែលឆ្លើយតបនឹងទ្វេគ្រោះនៃការរុករកនិងការចំរាញ់ដោយរក្សាឱកាស \(100\times\varepsilon\) ភាគរយក្នុងការរុករកដើម្បីបន្តប្រមូលពត៌មាន ប៉ុន្តែមិនចំណាយជំហានច្រើនពេកក្នុងការរុករកឡើយ។ ប្រមាណវិធីទាំង២នេះជាឧទាហរណ៍នៃការដោះស្រាយបញ្ហា \(k\)-armed bandit។

ដើម្បីប្រៀបធៀបគុណភាពនៃប្រមាណទាំង២ខាងលើ ខ្ញុំបានអនុវត្តពិសោធន៍លេខតូចមួយលើបញ្ហា \(2\)-armed bandit ដែលមានការកំណត់ដូចតទៅ។ ខ្ញុំជ្រើសយកគូ \((\mu_1=0.1, \mu_2=0.5)\)ជាការកំណត់នៃបញ្ហា (problem configuration) ហើយចំពោះ ETC ខ្ញុំជ្រើសទាញដៃនិមួយៗ ៤ដងមុននឹងប្តូរផ្តាច់។ ចំណែក \(\varepsilon\)-Greedy ខ្ញុំជ្រើសយក \(\varepsilon=0.1\)។ ជាលទ្ធផលពិសោធន៍លេខ រូបទី២(Figure 2)បង្ហាញពីរង្វាន់មធ្យមក្នុងមួយជំហាន ដែលប្រមាណវិធីនិមួយៗទទួលបាន។ លទ្ធផលនេះបង្ហាញថា \(\varepsilon\)-Greedy ល្អជាង ETC ហើយ \(\varepsilon\)-Greedy មានរង្វាន់មធ្យមក្នុងមួយជំហានខិតទៅក្បែរ (ប៉ុន្តែ តិចជាង) \(\mu_2=0.5\) ដែលជាអតិបរមានៃរង្វាន់មធ្យមក្នុងមួយជំហាន។

Figure 2: រូបទី២៖ រង្វាន់មធ្យមក្នុងមួយជំហាន ដែលប្រមាណវិធីនិមួយៗទទួលបានក្នុងបញ្ហា \(2\)-armed bandit ដែល \(\mu_1=0.1\) និង \(\mu_2=0.5\)។ អ័ក្សឈរបង្ហាញពីរង្វាន់មធ្យមក្នុងមួយជំហាននៃប្រមាណវិធីនិមួយៗ ឯអ័ក្សដេកបង្ហាញពីចំនួនជំហានដែលបានលេងហើយ។

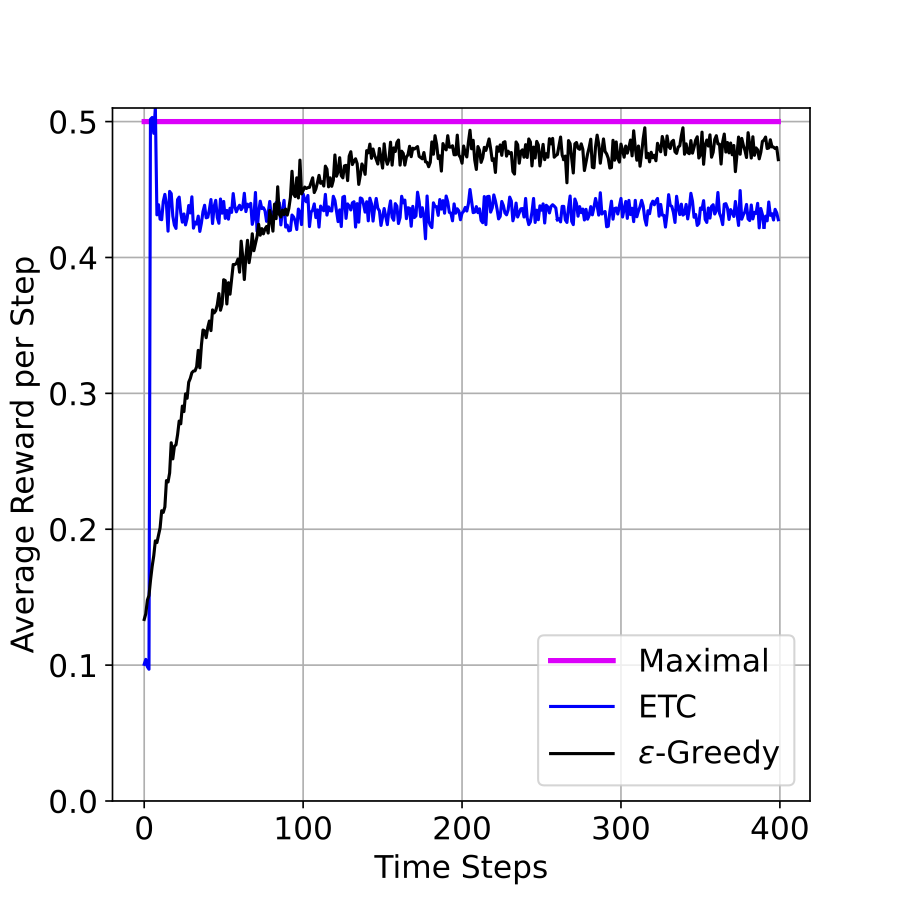
រង្វាស់គុណភាពនៃប្រមាណវិធី

ដើម្បីវាស់គុណភាពនៃប្រមាណវិធីណាមួយ អ្នកវិទ្យាសាស្រ្តអាចប្រើប្រាស់ទំហំមួយអោយឈ្មោះថា \(\text{Regret}\) ។ បើយើងស្គាល់តម្លៃសង្ឃឹម \(\\{\mu_i \\}_{1\le i\le k}\) នោះយើងអាចទទួលបានមធ្យមនៃរង្វាន់សរុបអតិបរមា ដោយគ្រាន់តែទាញដៃណាដែលមានសង្ឃឹមធំជាងគេ ហើយតម្លៃអតិបរមានោះស្មើ \(\max_i\mu_i T\) ដែល \(\max_i\mu_i\) ជាតម្លៃសង្ឃឹមធំជាងគេ។ អ្នកវិទ្យាសាស្រ្តកំណត់ \(\text{Regret}\) នៃប្រមាណវិធី \(\mathcal{A}\) ដោយ

\[\begin{equation} \text{Regret}(\mathcal{A}, T):=\max_i\mu_i T -\sum_{t=1}^T r_t \end{equation}\]

។ តាមនិយមន័យនេះ \(\text{Regret}\) របស់\(\varepsilon\)-Greedy ក្នុងពិសោធន៍ខាងលើគឺជាក្រឡាផ្ទៃខណ្ឌដោយបន្ទាត់ពណ៌ផ្កាឈូកនិងខ្សែកោងពណ៌ខ្មៅនៅក្នុងរូបទី២(Figure 2)។ ខ្ញុំបង្ហាញក្រឡាផ្ទៃនេះក្នុងរូបទី៣(Figure 3) ខាងក្រោម។

Figure 3: រូបទី៣៖ \(\text{Regret}\) មធ្យមនៃ\(\varepsilon\)-Greedy បង្ហាញដោយផ្ទៃក្រឡាផាត់ពណ៌ខ្មៅ។ អ័ក្សឈរបង្ហាញពីរង្វាន់មធ្យមក្នុងមួយជំហាននៃប្រមាណវិធីនិមួយៗ ឯអ័ក្សដេកបង្ហាញពីចំនួនជំហានដែលបានលេងហើយ។

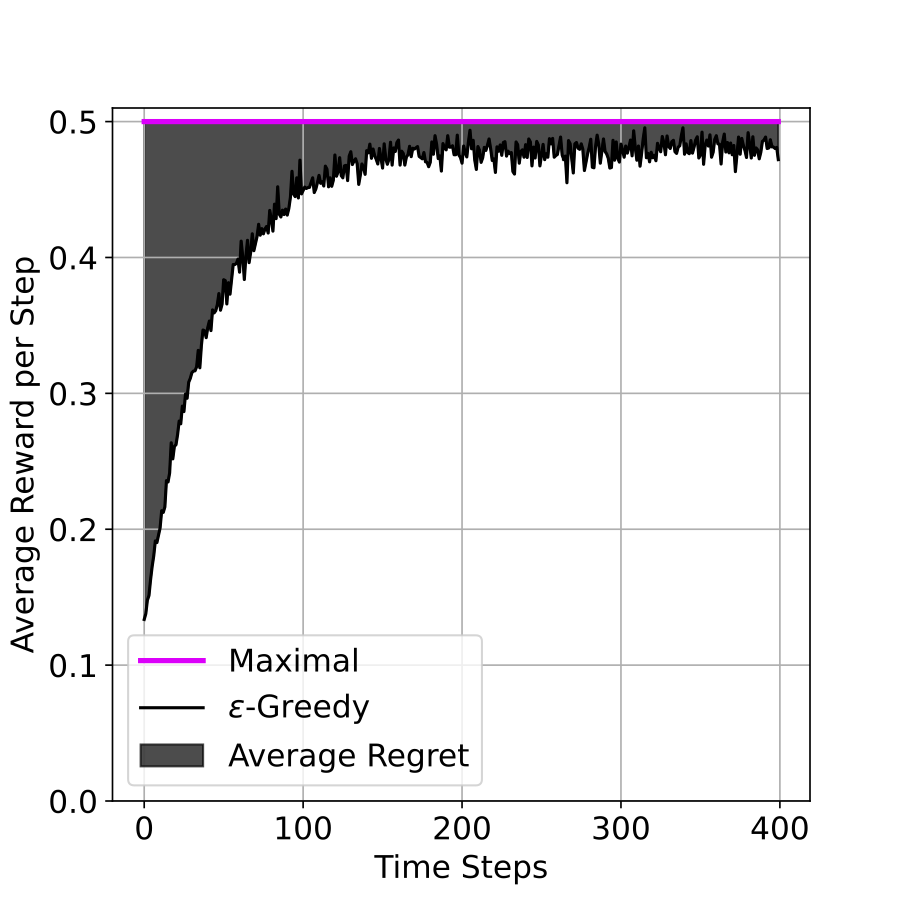
ទន្ទឹមនឹងនិយមន័យខាងលើនេះ រូបទី៤(Figure 4) បង្ហាញពី \(\text{Regret}\) មធ្យមនៃប្រមាណវិធី \(\varepsilon\)-Greedy និងETC ជាអនុគមន៍នៃជំហាន ក្នុងពិសោធន៍លេខដែលបានរៀបរាប់ខាងលើ។ តាមរយៈរូបទី៤(Figure 4) \(\text{Regret}\) នៃ\(\varepsilon\)-Greedy និងETC ជាអនុគមន៍លីនេអ៊ែរនៃជំហាន ពេលដែលចំនួនជំហានកាន់តែធំ ដែលគេនិយមសរសេរថា \(\text{Regret}\) ស្មើទៅនឹង \(O(T)\)។

Figure 4: រូបទី៤៖ \(\text{Regret}\) មធ្យមនៃប្រមាណវិធីនិមួយៗទទួលបានក្នុងបញ្ហា \(2\)-armed bandit ដែល \(\mu_1=0.1\) និង \(\mu_2=0.5\)។ អ័ក្សឈរបង្ហាញពី \(\text{Regret}\) មធ្យមក្នុងមួយជំហាននៃប្រមាណវិធីនិមួយៗ ឯអ័ក្សដេកបង្ហាញពីចំនួនជំហានដែលបានលេងហើយ។

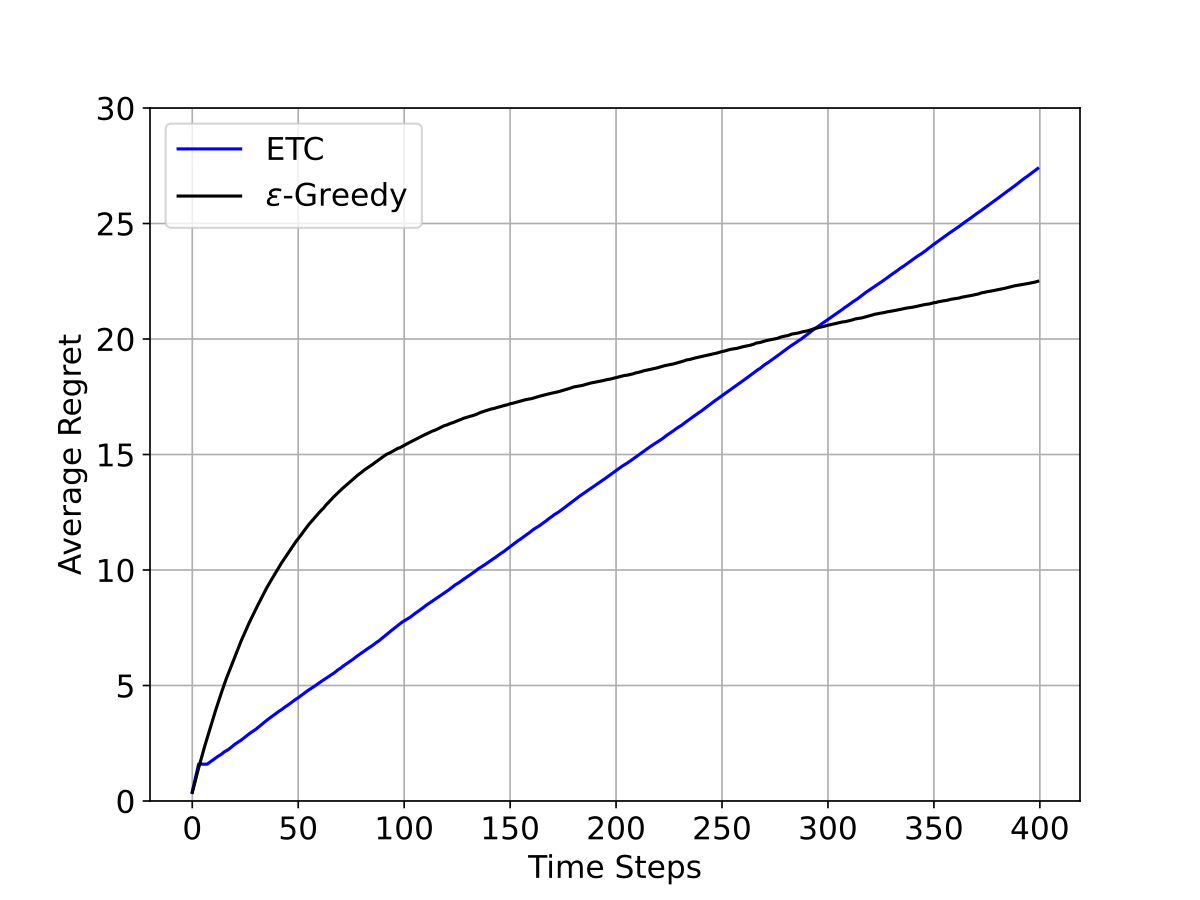
បើ \(\text{Regret}\) មធ្យមកាន់តែតូច នោះប្រមាណវិធីកាន់តែមានគុណភាពល្អ។ ទាញចេញពីរូបទី៣(Figure 3) ខាងលើ \(\text{Regret}\) មធ្យមកាន់តែតូច ប្រសិនបើរង្វាន់មធ្យមក្នុងមួយជំហានរបស់ប្រមាណវិធី កាន់តែឆាប់ខិតទៅជិតអតិបរមាននៃរង្វាន់មធ្យមក្នុងមួយជំហាន ដែលគេនិយមនិយាយថា ប្រមាណវិធីរៀនកាន់តែលឿន។ ជាទ្រឹស្តី គេចាត់ទុកថាប្រមាណវិធី \(\mathcal{A}\) មួយល្អប្រសើរ បើ \(\displaystyle\lim_{T\to+\infty} \frac{\text{Regret}(\mathcal{A}, T)}{T}=0\) (ឬគេអាចសរសេរ \(\text{Regret}(\mathcal{A}, T)= o(T)\))។ ប្រសិនបើករណីនេះពិត គេនិយាយថា \(\mathcal{A}\) ជាប្រមាណវិធី no-regret។ ដូចនេះ \(\varepsilon\)-Greedy និង ETC មិនមែនជាប្រមាណវិធី no-regret ឡើយ។ ក្នុងបញ្ហា multi-armed bandit អ្នកវិទ្យាសាស្រ្តចង់តាក់តែងប្រមាណវិធីណាដែលមាន \(\text{Regret}\) មធ្យមស្មើទៅនឹង \(O(T^\alpha)\) ដោយព្យាយាមធ្វើអោយ \(\alpha\) តូចតាមដែលអាចធ្វើទៅបាន។

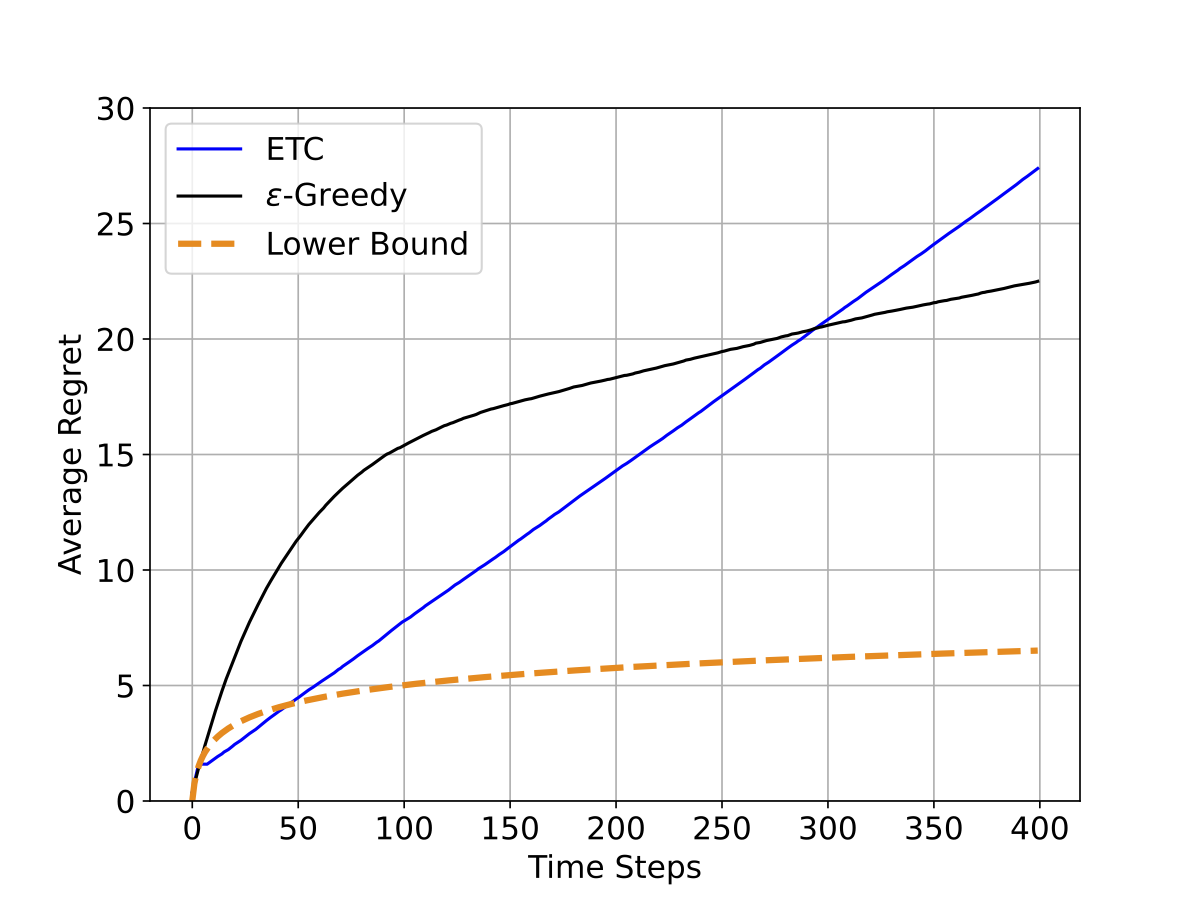
ដោយសារទ្វេគ្រោះនៃការរុករកនិងការចំរាញ់ ប្រមាណវិធីល្អ¹កម្រិតណាក៏ដោយ ក៏ត្រូវតែមានការខាតបង់ដែរ។ អ្នកស្រាវជ្រាវបានសិក្សាស្វែងរកកំហាតបង់អប្បបរមាដែលប្រមាណវិធីល្អមួយមិនអាចជៀសបាន។ ក្នុងនោះ (Lai and Robbins 1985) បានចងក្រងជាទ្រឹស្តីថា មានទំហំ \(c(\theta)\ln(T)\) ជាកំហាតបង់អប្បបរមា និងត្រូវបានគេអោយឈ្មោះថា ដែនទាល់ក្រោម (Lower bound)។ រូបទី៥(Figure 5) បង្ហាញពីដែនទាល់ក្រោមក្នុងពិសោធន៍ខាងលើ។ តាមរយៈរូបទី៥(Figure 5) ឥរិយាបថអាស៊ីមតូទីក (asymtotic behavior) របស់\(\varepsilon\)-Greedy និង ETC (ដែលមានរាងជាអនុគមន៍បន្ទាត់) មិនដូចនឹងដែនទាល់ក្រោមឡើយ (ដែលមានរាងជាអនុគមន៍លោការីត)។

យក \(\Theta\) ជាសំណុំមួយនៃការកំណត់បញ្ហា (set of problem configurations)។ បើប្រមាណវិធី \(\mathcal{A}\) មួយមានលក្ខណៈល្អជាឯកសណ្ឋាន (uniformly efficient) លើសំណុំ \(\Theta\) នោះរាល់ការកំណត់បញ្ហា \(\theta\in\Theta\) \[ \text{Regret}(\mathcal{A}, T) \ge c(\theta)\ln(T) \] ដែល \(c(\theta)\) ជាចំនួនថេរមួយអាស្រ័យនឹង \(\theta\)។

តាមរយៈទ្រឹស្តីនេះ គ្មានអ្នកវិទ្យាសាស្រ្តណាអាចតាក់តែងប្រមាណវិធីល្អមួយដែលមាន \(\text{Regret}\) ស្មើនឹង \(o(\ln T)\) ក្នុងរាល់ការកំណត់បញ្ហាឡើយ។ ដូចនេះ ប្រមាណវិធីណាដែលមាន \(\text{Regret}\) ស្មើនឹង \(O(\ln T)\) ក្នុងរាល់ការកំណត់បញ្ហា នឹងត្រូវបានគេហៅថា ប្រមាណវិធីដែលអាស៊ីមតូទិកខលលីអុបធីម៉ល (asymptotically optimal)។

*សម្គាល់: ប្រមាណវិធី \(\mathcal{A}\) ល្អជាឯកសណ្ឋាន (uniformly efficient) លើសំណុំ \(\Theta\) មានន័យថា រាល់ការកំណត់បញ្ហា \({\theta\in\Theta}\), \(\text{Regret}(\mathcal{A},T)=O(T^{\alpha})\) ដែល \(\alpha\in(0,1)\) ឬនិយាយម៉្យាងទៀតថា \(\mathcal{A}\) ជាប្រមាណវិធី no-regret ក្នុងរាល់ការកំណត់បញ្ហា \({\theta\in\Theta}\) ។

Figure 5: រូបទី៥៖ \(\text{Regret}\) មធ្យមនៃប្រមាណវិធីនិមួយៗទទួលបានក្នុងបញ្ហា \(2\)-armed bandit ដែល \(\mu_1=0.1\) និង \(\mu_2=0.5\)។ ខ្សែកោងពណ៌ទឹកក្រូចដាច់ៗបង្ហាញពីដែនទាល់ក្រោមនៃការកំណត់បញ្ហានេះ។

សន្និដ្ឋាន

នៅក្នុងអត្ថបទនេះ ខ្ញុំបានរៀបរាប់អំពី Multi-armed bandit ដែលជាបញ្ហាបង្កប់នូវទ្វេគ្រោះនៃការរុករកនិងការចំរាញ់។ ដើម្បីវាស់វែងការដោះដូរ (tradeoff) រវាងការរុករក និងការចំរាញ់ ឬគុណភាពរបស់ប្រមាណវិធីណាមួយ គេអាចប្រើប្រាស់ទំហំអោយឈ្មោះថា \(\text{Regret}\)។ កម្រិតល្អជាអប្បបរមានៃរាល់ប្រមាណវិធីត្រូវបានកំណត់ដោយដែនទាល់ក្រោមនៃ \(\text{Regret}\)។ ក្នុងអត្ថបទក្រោយ ខ្ញុំនឹងនិយាយអំពីវិធីសាស្រ្តមួយដែលសាកល្បងដោះស្រាយទ្វេគ្រោះនៃការរុករកនិងការចំរាញ់៕

ឯកសារយោង

Lai, Tze Leung, and Herbert Robbins. 1985. “Asymptotically Efficient Adaptive Allocation Rules.” Advances in Applied Mathematics 6 (1): 4–22.

Lattimore, Tor, and Csaba Szepesvári. 2020. Bandit Algorithms. Cambridge University Press.

Simchi-Levi, David, and Chonghuan Wang. 2023. “Multi-Armed Bandit Experimental Design: Online Decision-Making and Adaptive Inference.” In International Conference on Artificial Intelligence and Statistics, 3086–97. PMLR.

Thompson, William R. 1933. “On the Likelihood That One Unknown Probability Exceeds Another in View of the Evidence of Two Samples.” Biometrika 25 (3/4): 285–94.

Footnotes

1. ពាក្យ “ល្អ” ត្រង់នេះចង់សំដៅថាល្អជាឯកសណ្ឋាន ដែលមិនថាការកំណត់របស់បញ្ហាបែបណាទេ(for any problem configurations) ក៏ប្រមាណវិធីនោះមាន Regret ស្មើនឹង \(O(T^\alpha)\) ដោយ\(\alpha<1\) (សូមមើលសម្គាល់ខាងលើ)។