Scence Text Recognition with Permuted Autoregressive Sequence Models
Abstract
I want to re-implement PARSeq (Bautista and Atienza (2022)) (https://github.com/baudm/parseq) for Khmer text. Using Kimang18/khmer-hanuman-small-images, I got cer of \(70\%\) which is not sufficiently good compared to the performance of PARSeq presented in their paper.
Introduction
PARSeq is a method to solve the task of recognizing text from the cropped regions in natural scenes. This method achieves state-of-the-art (SOTA) results in STR benchmarks (\(91.9\%\) accuracy) by just using synthetic training data Bautista and Atienza (2022).
Core Idea
In sequence modeling, deep learning models are trained to generate future tokens conditioned on past tokens. Consequently, the models become \[ \mathbb{P}(\mathbf{y}|\mathbf{x}) =\prod_{t=1}^T\mathbb{P}(y_t|\mathbf{y}_{<t}, \mathbf{x}) =p(y_1|\mathbf{x})\times p(y_2|y_1, \mathbf{x})\times p(y_3|y_2, y_1, \mathbf{x})\times \dots \times p(y_T|y_{T-1},\dots, y_1, \mathbf{x}) \tag{1}\] where \(\mathbf{y}\) is the \(T\)-length text label of the image \(\mathbf{x}\). This method is known as monotonic autoregressive generation. We want to find parameter \(\theta^*\) that maximizes Equation 1 \[\begin{equation} \log \mathbb{P}_{\theta^*}(\mathbf{y} | \mathbf{x}) = \max_{\theta}\sum_{t=1}^T\log p_{\theta}(y_t|\mathbf{y}_{<t}, \mathbf{x}) \end{equation}\]
PARSeq method is an adaptation of Permutation Language Modeling (PLM) (Yang et al. (2019)) for Scene Text Recognition (STR). Let \({\mathcal{Z}}_T\) be the set of all possible permutations of \(\{1,2,\dots,T\}\). Without loss of generality, we will fix \(T\) and omit it from the expression if possible. Let \({\mathbf{z}}\in{\mathcal{Z}}\) be a permutation that specify an ordering of the text label \({\mathbf{y}}\) and define
\[\begin{align*} \mathbb{P}(\mathbf{y}_{{\mathbf{z}}}|\mathbf{x}) &=p(y_{z_1}|\mathbf{x})\times p(y_{z_2}|y_{z_1}, \mathbf{x})\times p(y_{z_3}|y_{z_2}, y_{z_1}, \mathbf{x})\times \dots \times p(y_{z_T}|y_{z_{T-1}},\dots, y_{z_1}, \mathbf{x}) \\ &=\prod_{t=1}^Tp(y_{z_t}|{\mathbf{y}}_{{\mathbf{z}}_{<t}}{\mathbf{x}}) \end{align*}\] So, Equation 1 is the case where \(z_t=t, \forall t\le T\).
PARSeq method wants to find \(\theta^*\) that maximizes
\[ \log \mathbb{P}_{\theta^*}({\mathbf{y}}| {\mathbf{x}}) = \max_{\theta}{\mathbb{E}}_{{\mathbf{z}}\in{\mathcal{Z}}}\left[\sum_{t=1}^T\log p_{\theta}(y_{z_t}|\mathbf{y}_{z_{<t}}, \mathbf{x})\right] \tag{2}\]
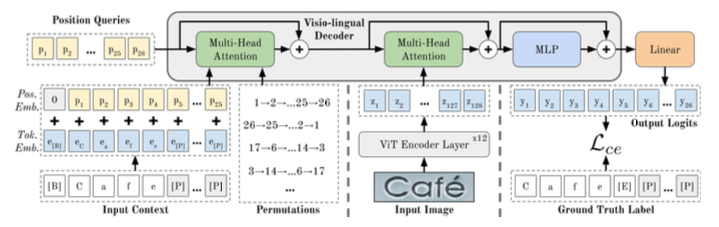
It is clear that PARSeq is more general than monotonic autoregressive method that execute the prediction in only one direction, namely left-to-right. Moreover, the objective function Equation 2 only requires modification on Visio-lingual Decoder (Image Encoder can follow similarly to Vision Transformer architecture). An overview of PARSeq architecture and training process is given in Figure 1.
Objective Function
Let \({\mathbf{e}}\in{\mathbb{R}}^{T\times d_m}\) be the token embedding of \({\mathbf{y}}\in{\mathbb{R}}^T\), \({\mathbf{p}}\in{\mathbb{R}}^{T\times d_m}\) be the position embedding and \({\mathbf{c}}:={\mathbf{e}}+{\mathbf{p}}\) be the context embedding. \(d_m\) is the embedding dimension. Let \({\mathbf{M}}_k\) be the attention mask that reflect the permutation \({\mathbf{z}}_k\) (e.g. if \(\forall t\le T, z_{k,t}=t\), then the corresponding mask is just the causal mask for left-to-right direction). The model \(f({\mathbf{x}}, {\mathbf{p}}, {\mathbf{c}}, {\mathbf{M}})\) outputs logits in space \({\mathbb{R}}^{(T+1)\times(S+1)}\) where \(S\) is the size of character set (charset) used for training with additional character pertaining to \([E]\) token (which marks the end of sequence). Applying softmax on the logits, we get the probability distribution over charset.
The loss for a given \({\mathbf{M}}_k\) is just a cross-entropy loss \({\mathcal{L}}_{ce}\left({\mathbf{y}}, f({\mathbf{x}}, {\mathbf{p}}, {\mathbf{c}}, {\mathbf{M}}_k)\right)\) and the final loss is given by \[ {\mathcal{L}}=\frac{1}{K}\sum_{k=1}^K{\mathcal{L}}_{ce}\left({\mathbf{y}}, f({\mathbf{x}}, {\mathbf{p}}, {\mathbf{c}}, {\mathbf{M}}_k)\right) \tag{3}\]
So, the main implementation is to generate permutation \({\mathbf{z}}_k\) and the corresponding attention mask \({\mathbf{M}}_k\) for \(1\le k\le K\).
Tricks in Implementation
There are two tricks to make the PARSeq’s implementation more feasible:
- Manipulate Attention Mask
- Use empirical version of Equation 2
Manipulate Attention Mask
In PARSeq, the position tokens encode the target position to be predicted, each one having a direct correspondence to a specific position in the output. The model uses position tokens as the query for the attention mechanism, word combined with position tokens as context embedding (namely, key and value), and mask attention to reflect the ordering specified by permutation. Using position tokens as the query allows the model to learn meaningful pattern from PLM(Bautista and Atienza (2022)). This is different from standard AR model where context embedding as the query (aka self-attention mechanism).
| \([B]\) | \(c_1\) | \(c_2\) | \(c_3\) | |
|---|---|---|---|---|
| \(p_1\) | 0 | \(-\inf\) | \(-\inf\) | \(-\inf\) |
| \(p_2\) | 0 | 0 | \(-\inf\) | \(-\inf\) |
| \(p_3\) | 0 | 0 | 0 | \(-\inf\) |
| \(p_4\) | 0 | 0 | 0 | 0 |
| \([B]\) | \(c_1\) | \(c_2\) | \(c_3\) | |
|---|---|---|---|---|
| \(p_1\) | 0 | \(-\inf\) | 0 | 0 |
| \(p_2\) | 0 | \(-\inf\) | \(-\inf\) | 0 |
| \(p_3\) | 0 | \(-\inf\) | \(-\inf\) | \(-\inf\) |
| \(p_4\) | 0 | 0 | 0 | 0 |
| \([B]\) | \(c_1\) | \(c_2\) | \(c_3\) | |
|---|---|---|---|---|
| \(p_1\) | 0 | \(-\inf\) | \(-\inf\) | \(-\inf\) |
| \(p_2\) | 0 | 0 | \(-\inf\) | 0 |
| \(p_3\) | 0 | 0 | \(-\inf\) | \(-\inf\) |
| \(p_4\) | 0 | 0 | 0 | 0 |
| \([B]\) | \(c_1\) | \(c_2\) | \(c_3\) | |
|---|---|---|---|---|
| \(p_1\) | 0 | \(-\inf\) | 0 | 0 |
| \(p_2\) | 0 | \(-\inf\) | \(-\inf\) | \(-\inf\) |
| \(p_3\) | 0 | \(-\inf\) | 0 | \(-\inf\) |
| \(p_4\) | 0 | 0 | 0 | 0 |
Use Empirical version of Equation 2
For \(T\)-length text label, there are \(T!\) factorizations of likelihood as Equation 2. This is not practical as \(T\) tends to be large in practice. Moreover, doing \(T!\) factorizations does not always guarantee better performance (Bautista and Atienza (2022)) and could cause training instability. So, the author makes a compromise by choosing only \(K=6\) permutations including left-to-right and right-to-left directions.
Implementation
Mixed-Precision Training
I will use ready-implemented layers in PyTorch. However, those layers are implemented for float32. Since I use bfloat16, I need to re-implement those layers by casting dtype accordingly. If you do not use mixed-precision training, you can ignore the code in this section.
from typing import Optional, Sequence
import torch, torch.nn as nn
from torch import Tensor
from dataclasses import dataclass
class RMSNorm(nn.RMSNorm):
def forward(self, x):
return super().forward(x.float()).type(x.dtype)
class Linear(nn.Linear):
def forward(self, x: Tensor) -> Tensor:
return F.linear(x, self.weight.to(x.dtype), None if self.bias is None else self.bias.to(x.dtype))
class MultiheadAttention(nn.MultiheadAttention):
def forward(self, query, key, value, key_padding_mask=None, need_weights=False, attn_mask=None):
z1, z2 = super().forward(query.float(), key.float(), value.float(), need_weights=need_weights, key_padding_mask=key_padding_mask, attn_mask=attn_mask)
return z1.type(query.dtype), z2
@dataclass
class ModelConfig:
img_size: Sequence[int]
patch_size: Sequence[int]
n_channel: int
vocab_size: int
block_size: int
n_layer: int
n_head: int
n_embed: int
dropout: float = 0.0
bias: bool = TrueImage Encoder
To facilitate code readibility, I use Vision Transformer implemented in PyTorch for Image Encoder of PARSeq. I follow PARSeq paper by taking image size as \((128, 32)\) and patch size as \((8, 4)\). So, patch embedding outputs \(\frac{128}{8}\times \frac{32}{4}=128\) tokens, each token is a vector of size \(d_{m}\).
from timm.models.vision_transformer import PatchEmbed, VisionTransformer
class ImageEncoder(VisionTransformer):
def __init__(self, config):
super().__init__(
img_size=config.img_size,
patch_size=config.patch_size,
in_chans=config.n_channel,
embed_dim=config.n_embed,
depth=config.n_layer,
num_heads=config.n_head,
mlp_ratio=4,
qkv_bias=True,
drop_rate=0.0,
attn_drop_rate=0.0,
drop_path_rate=0.0,
embed_layer=PatchEmbed,
num_classes=0, # These
global_pool='', # disable the
class_token=False, # classifier head.
)
def forward(self, x):
return self.forward_features(x)Residual Attention Block
I design this block for self-attention and causal cross-attention.
import torch.nn as nn
class ResidualAttentionBlock(nn.Module):
def __init__(self, n_embed, n_head, n_mlp, dropout=0.0, bias=True, activation=None, cross_attn=False):
super().__init__()
self.n_embed = n_embed
self.n_head = n_head
self.dropout1 = nn.Dropout(dropout)
self.mha = MultiheadAttention(n_embed, n_head, dropout=dropout, bias=bias, batch_first=True)
self.dropout2 = nn.Dropout(dropout)
self.cross_ln = RMSNorm(n_embed) if cross_attn else None
self.cross_mha = MultiheadAttention(n_embed, n_head, dropout=dropout, bias=bias, batch_first=True) if cross_attn else None
self.ln = RMSNorm(n_embed)
self.ffn = nn.Sequential(
Linear(n_embed, n_mlp, bias=bias),
nn.GELU(approximate='tanh'),
nn.Dropout(dropout),
Linear(n_mlp, n_embed, bias=bias)
)
def forward(self, x, ctx, xi, key_mask, attn_mask):
"""
x: normalized query tensor (b, t, n_embed)
ctx: normalized context tensor (b, t, n_embed)
xi: normalized image feature tensor (b, t, n_embed)
"""
b, t, _ = x.size()
residual = x
x, _ = self.mha(query=x, key=ctx, value=ctx, key_padding_mask=key_mask, need_weights=False, attn_mask=attn_mask)
x = residual + self.dropout1(x)
if self.cross_mha:
residual = x
x = self.cross_ln(x)
x, _ = self.cross_mha(query=x, key=xi, value=xi, need_weights=False)
x = residual + self.dropout2(x)
residual = x
x = self.ln(x)
x = self.ffn(x)
x = residual + x
return xVisio-lingual Decoder
For visio-lingual decoder, the heavy task is to implement attention mask according to the position permutation. As shown in Table 1, the first column of the mask is for bos. Since any positions must communicate with bos token, the first column of any attention masks here is all zero. Moreover, the position corresponding to eos target token must communicate with all context tokens. So, the last row of any attention masks here is all zero. However, it is possible that the last position tokens correspond to pad target token. In such case, handle_eos_masking function makes sure that the positions corresponding to eos target token communicate with all context tokens.
def generate_k_permutations(n, k):
"""
Generates K unique permutations of the sequence [0, 1, ..., n-1].
Args:
n (int): The upper bound of the range (0 to n-1).
k (int): The number of permutations to generate.
Returns:
list: A list containing K lists, each being a unique permutation.
"""
# Create the base sequence
base_list = list(range(n))
# Use a set to ensure we get unique permutations if K is large
# relative to the total possible permutations (n!)
permutations = set([tuple(base_list), tuple(reversed(base_list))])
# Calculate n factorial to prevent infinite loops if K > n!
max_possible = math.factorial(n)
if k > max_possible:
raise ValueError(f"Requested {k} permutations, but only {max_possible} exist for n={n}.")
while len(permutations) < k:
# random.sample creates a new shuffled list without mutating the original
perm = random.sample(base_list, len(base_list))
permutations.add(tuple(perm))
permutations.add(tuple(reversed(perm)))
return [list(p) for p in permutations]
def generate_mask(permutation: Tensor):
sz = permutation.size(0)
mask = torch.full((sz, sz), fill_value=float('-inf'), device=permutation.device)
for i in range(sz):
mask[permutation[i], permutation[:i]] = 0.0
return mask
def handle_eos_masking(condition: Tensor, mask: Tensor, n_head: int):
b, t = condition.size()
mask = mask.expand(b, -1, -1)
condition = condition.unsqueeze(-1).bool()
mask = torch.where(condition, torch.tensor(0.0), mask)
return mask.repeat_interleave(n_head, dim=0)
class TextDecoder(nn.Module):
def __init__(self, config) -> None:
super().__init__()
self.config = config
self.n_head = 2 * config.n_head
self.tok_embed = nn.Embedding(config.vocab_size, config.n_embed)
self.pos_embed = nn.Embedding(config.block_size, config.n_embed)
self.ln_pos = RMSNorm(config.n_embed)
self.dropout = nn.Dropout(config.dropout)
self.blocks = nn.ModuleList(
[ResidualAttentionBlock(config.n_embed, self.n_head, 4 * config.n_embed, config.dropout, config.bias, cross_attn=True)
for _ in range(1)]
)
self.ln_f = RMSNorm(config.n_embed)
self.lm_head = Linear(config.n_embed, config.vocab_size, bias=False)
# weight tying
self.tok_embed.weight = self.lm_head.weight
mask = nn.Transformer.generate_square_subsequent_mask(config.block_size)
self.register_buffer("mask", mask)
if self.tok_embed.weight.device.type == 'cuda':
self.tok_embed.weight = self.tok_embed.weight.to(torch.bfloat16)
self.pos_embed.weight = self.pos_embed.weight.to(torch.bfloat16)
def forward(self, x, xi, targets=None):
b, t = x.size()
pos_embed = self.pos_embed(torch.arange(0, t, device=x.device)) # exclude bos pos
pos_embed = pos_embed.expand(b, -1, -1) # (b, t, n_embed)
tok_embed = self.tok_embed(x) * np.sqrt(self.config.n_embed) # (b, t, n_embed)
bos_embed = tok_embed[:, :1]
ctx = torch.cat([bos_embed, tok_embed[:, 1:] + pos_embed[:, :-1]], dim=1) # start from bos token
ctx = self.dropout(F.rms_norm(ctx, (ctx.size(-1), ))) # (b, t, n_embed)
pos_embed = self.dropout(self.ln_pos(pos_embed))
if targets is not None:
key_mask = torch.zeros((b, t), device=x.device)
key_mask[targets < 0] = float('-inf')
condition = targets == tokenizer.eos_id
if t-1 > 2:
permutations = generate_k_permutations(t-1, 6)
else:
permutations = generate_k_permutations(t-1, 2)
loss = 0.0
for perm in permutations:
attn_mask = torch.zeros((t, t), device=x.device)
attn_mask[:-1, 1:] = generate_mask(torch.tensor(perm, device=x.device))
attn_mask = handle_eos_masking(condition, attn_mask, self.n_head)
logits = self.logits(pos_embed.clone(), ctx, xi, attn_mask=attn_mask, key_mask=key_mask)
loss += F.cross_entropy(logits.view(-1, logits.size(-1)), targets.view(-1), ignore_index=-100, reduction='mean')
loss = loss / len(permutations)
return logits, loss
else:
mask = self.mask[:t, :t]
return self.logits(pos_embed, ctx, xi, mask), _
def logits(self, query, ctx, xi, attn_mask, key_mask=None):
for block in self.blocks:
query = block(query, ctx=ctx, xi=xi, attn_mask=attn_mask, key_mask=key_mask)
query = self.ln_f(query)
return self.lm_head(query).float()PARSeq Model
Now, we can finally write PARSeqModel class where image encoder is a Vision Transformer and text decoder is a single Residual Attention Block. When deploy, we also need to develop decode function that outputs text in a given cropped region.
class PARSeqModel(nn.Module):
def __init__(self, config):
super().__init__()
self.encoder = ImageEncoder(config)
self.encoder = TextDecoder(config)
def forward(self, img_tensor: Tensor, inp_tokens: Tensor, tgt_tokens: Tensor=None):
xi = self.encoder(img_tensor)
logits, loss = self.decoder(inp_tokens, xi, tgt_tokens)
return logits, loss